

Explain different types of data in statistics.Find a rational number between 1/2 and 3/4.Three times the first of three consecutive odd integers is 3 more than twice the third.Find the sum of first 50 natural numbers.What is the probability of getting a sum of 9 when two dice are thrown simultaneously?.What is the probability sample space of tossing 4 coins?.Difference between an Arithmetic Sequence and a Geometric Sequence.If one-third of one-fourth of a number is 15, then what is the three-tenth of that number?.How many types of number systems are there?.What are some Real Life Applications of Trigonometry?.
SURFACE AREA OF A PRISM HOW TO

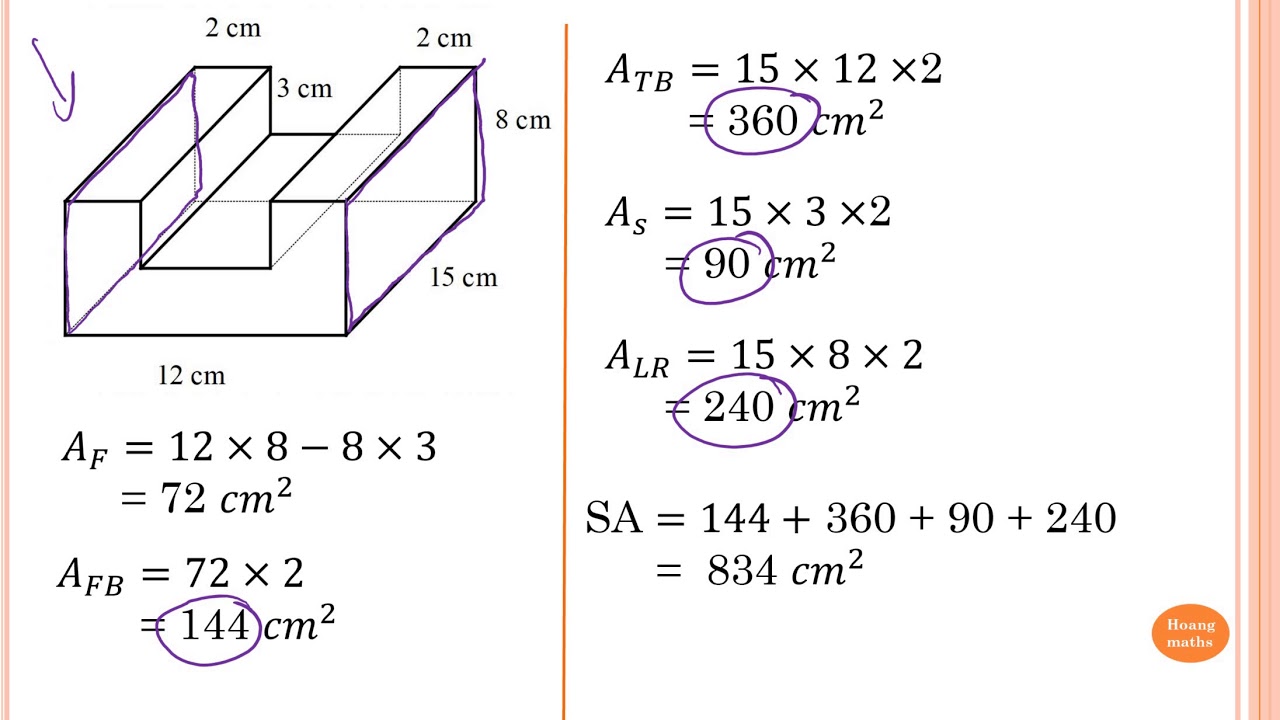
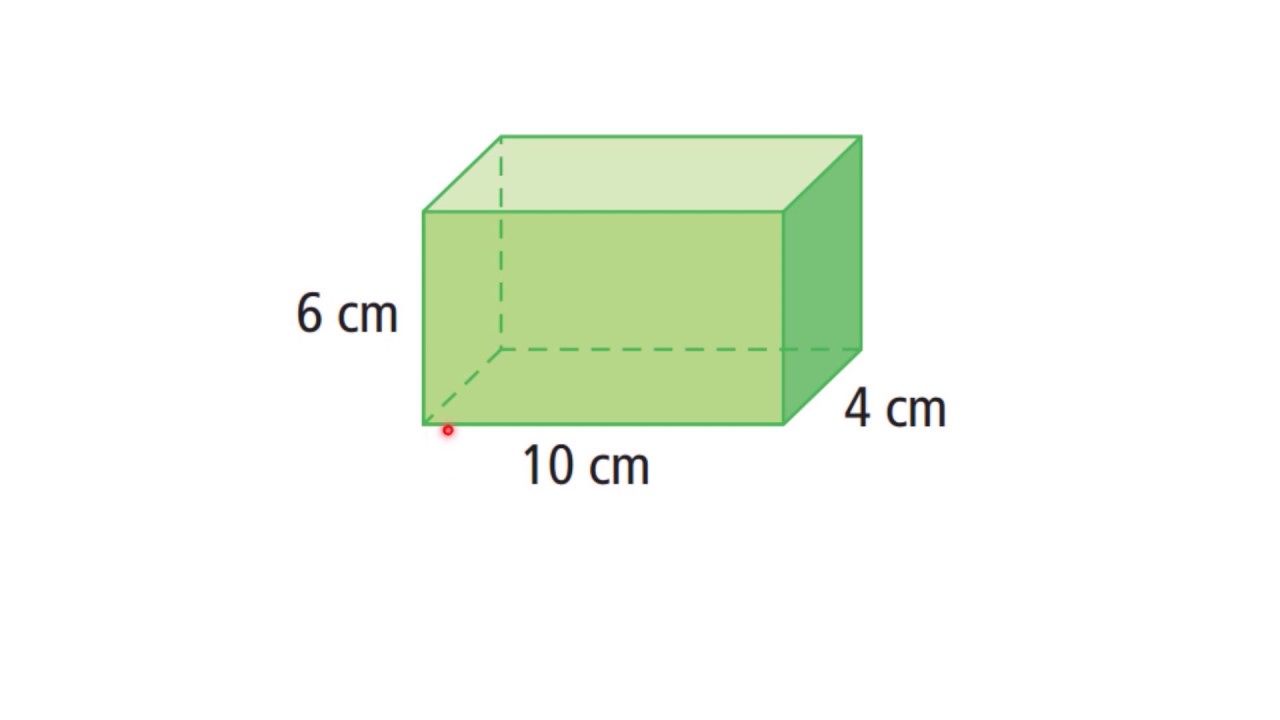
Surface area of the cylindrical part = 2πr (r + h)īut, one circular face of the cylinder is hidden. Surface area of the rectangular part = 2(lw + lh + wh) Calculate the surface area irregular solid. The length, width, and height of the rectangular part are 15 cm, 8 cm, and 4 cm, respectively. In the diagram below, the cylindrical part’s radius and height are 7 cm and 10 cm, respectively. Therefore, the surface area of an irregular solid can be calculated by adding together the regular objects’ surface areas that form it. The surface area of a sphere, SA = 4 πr 2įor a solid hemisphere, the surface area, SA = 3πr 2 Surface area of irregular solidsĪn irregular object is a combination of two or more regular objects. Where, b = base length and s = slant height. Where p = perimeter of the base and s = slant height of a pyramid.įor, a square pyramid, the surface area, SA = b 2 + 2bs The general formula for the surface area of a solid pyramid is: Just like a prism, a pyramid is named after the shape of its base. Where s is the slant height of a cone and r is the radius of the circular base.Ī pyramid can be defined as a solid with a polygonal base and triangular lateral faces. Surface area of a solid cone = Area of sector + area of a circle Surface area of a solid cylinder = 2πr (r + h)Ī cone is a solid with a circular base connected to a curved surface that tapers from the base to the top. Surface area of a cylinder = 2 × area of circle + area of a rectangle (the curved surface) The general formula for the surface area of a prism = 2 × area of the base + perimeter of base × height.Ī solid cylinder is an object with two parallel and congruent circular faces connected by a curved surface. The formula for the surface area for a prism depends on the shape of its base. Where, l = length, w = width and h = height of the solid.Ī prism is a three-dimensional solid with two parallel and congruent polygonal bases connected by rectangular faces. Surface area of a cuboid = 2lw + 2lh + 2wh
Regular solids have definite formulas for finding their surface areas.Ĭommon examples of regular solids include cubes, prisms, cuboids, spheres, hemispheres, cones, and cylinders. This article will discuss how to find the surface area of solids, the surface area of regular solids, and irregular solids’ surface area. To determine the surface area of a solid, we take the sum of the area of all the surfaces of a 3-dimensional solid object. Surface Area of a Solid – Explanation & Examples How to Find the Surface Area of a Solid?


 0 kommentar(er)
0 kommentar(er)
